Als ich in meiner Amateurzeit begann, mich mit Bildbearbeitung zu beschäftigen, hörte ich oft mystisch anmutende Worte wie „Frequenztrennung“ und „Wavelets“, die mein Interesse magisch anzogen. In diversen Büchern fand ich diese Dinge nur ansatzweise beschrieben. Durch mein Informatikstudium kannte ich diese gewaltigen Methoden aus der Signalverarbeitung und es fasziniert mich, diese Techniken für die Bearbeitung von Bildern einzusetzen.
Grundsätzlich wird dabei das Foto mit komplexen mathematischen Operationen in verschiedene Schichten, sogenannte Detailebenen zerlegt.
Hier habe ich das Foto mit den Tintenfässern in 12 Detailebenen zerlegt. Dieser 12 Ebenen entsprechen den Bildern \mathrm{B}_0, \mathrm{B}_1, \mathrm{B}_2 aus den mathematischen Grundlagen, allerdings haben wir jetzt 12 Stück davon. Als Summe dieser 12 Detailebenen würden wir wieder das Ausgangsfoto erhalten. Die Grundidee der frequenzseparierten Retusche besteht darin, die Ebenen zu verstärken, abzuschwächen und mit den üblichen Werkzeugen zu bearbeiteten und dann die bearbeiteten Ebenen zusammenzuführen.
Erste praktische Erfahrungen konnte ich mit RawTherapee sammeln. Ich fand das Waveletwerkzeug dort aber unzureichend. Ich konnte komplette Detailebenen verstärken oder abschwächen, allerdings konnte ich nicht einzelne Bereiche wie z.B. das Brautkleid bearbeiten.
Nach längerem Experimentieren konnte ich schließlich die Detailebenen berechnen und mit den Werkzeugen wie Kopierstempel und Ebenentechnik zu bearbeiten. Neben der umständlichen Handhabung zeigten sich jedoch bald Probleme: die Berechnung führte zu deutlichen Tonwertabrissen und leider auch zu einem gewissen Schärfeverlust, der mit meinen Qualitätsansprüchen nicht vereinbar ist. Durch das Zerlegung und Zusammenfügen der Detailebenen beobachtete ich teilweise Abweichungen der Farb- und Helligkeitswerte von 3-5%. Diese Probleme kamen durch die Anhäufung von Rundungsfehlern bei der Berechung der Wavelets mit 8bit-Ganzzahlen zustande.
So brauchte ich schließlich eine Möglichkeit, um Wavelets mit hoher numerische Präzision zu berechnen und zu bearbeiten. Da ich hierzu nichts passendes fand, musste ich auf meine Kenntnisse als Informatiker und Mathematiker zurückgreifen und selbst programmieren. Dabei wollte ich alle technischen Abläufe weitgehend automatisieren, um mich auf künstlerische Aspekte zu konzentrieren. Die Arbeiten zogen sich immer weiter in die Länge, durch einen privaten Umzug und Homeschooling wurde ich immer wieder aufgehalten.
Im Herbst 2020 konnte ich meinen Traum verwirklichen: nach einem größeren Einarbeitungsaufwand, Programmierung in G’MIC, der Entwickling von tcsh- und Pythonskripten kann ich nun Wavelets mit 32bit-Gleitkommazahlen, also mit hoher numerischer Präzision, berechnen und vollautomatisch in Gimp importieren.
Auch nach über 2 Jahren in der Anwendung ist dieser Prozess immer noch beeindruckend. Bei der Zerlegung eines einzigen Fotos heulen die Lüfter unter der enormen CPU-Last für mehrere Minuten auf, während die Prozessorkerne Milliarden von Zahlen durch arithmetische Prozesse laufen lassen. Die Detailebenen haben trotz LZW-Kompression eine Größe von mehreren Gigabyte und werden dann automatisch in Gimp importiert. Die Arbeit unter Gimp sieht üblicherweise so aus:
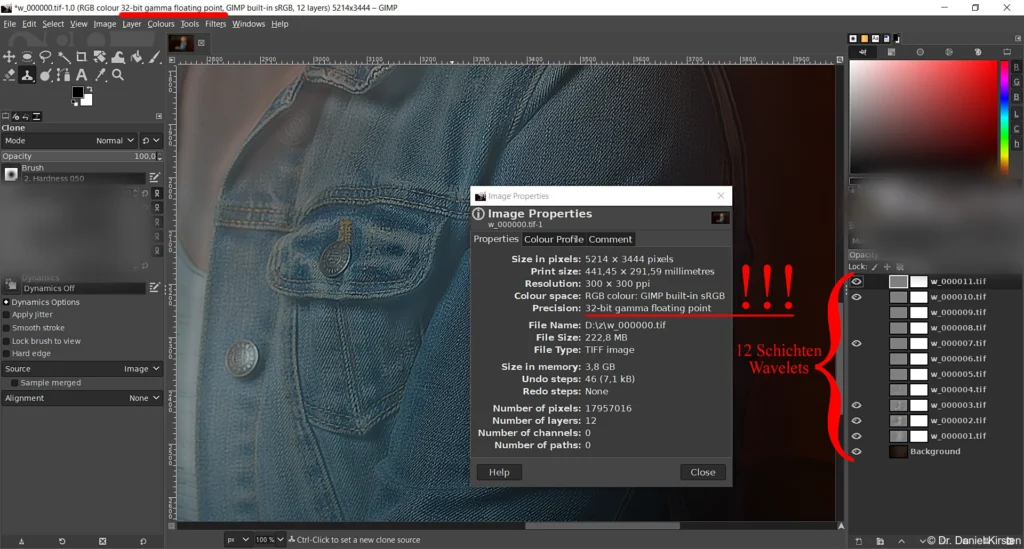
Die ganzen Berechnungen haben aber nur die Grundlage für die nun folgende künstlerische Tätigkeit geschaffen. Ich habe jetzt enorme Möglichkeiten durch das Bearbeiten der einzelnen Schichten, wobei allerdings auch ein mathematisches Hintergrundwissen vorteilhaft ist. Nach dem Abschluss der Bearbeitung werden die Schichten automatisch zusammengeführt und exportiert.



