Mathematische Grundlagen
Wir betrachen hier der Einfachheit halber nur den eindimensionalen Fall, die Theorie lässt sich recht leicht auf zwei- oder mehrdimensionale Funktionen erweitern. Unsere Bilder sind hier Abbildungen von \mathbb{R} nach \mathbb{R}. Betrachten wir nun als Beispiel ein Bild \mathrm{B}, welches der Gleichung
\newcommand{\B}{\textrm{B}}\begin{equation*} \B(x)\,=\,0.1\sin(20x)+0.3\sin(x)+0.16x-0.96 \end{equation*}
entspricht.
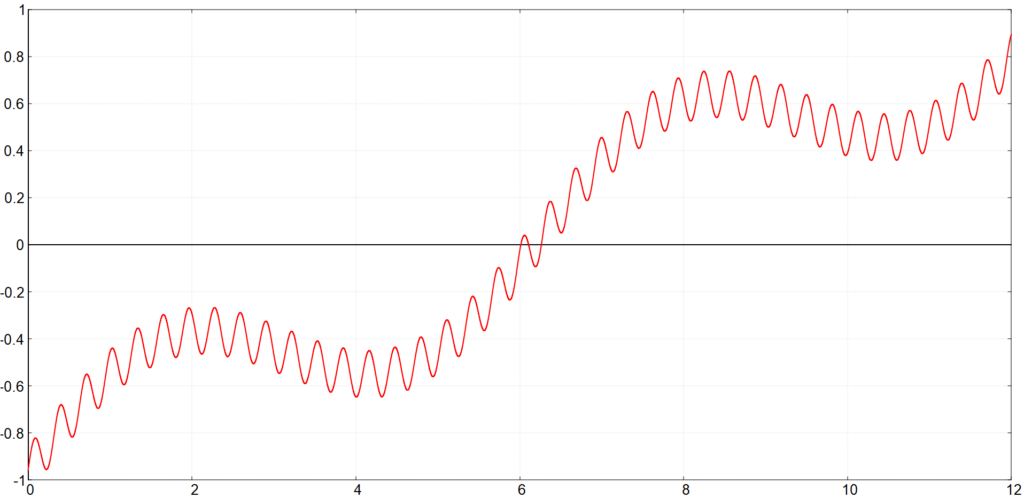
Wir können gut erkennen, dass sich in \mathrm{B} drei Strukturen überlagern. Wir erkennen 38 sehr feine Wellen, diese Wellen sind feine Details, z.B. Poren, die in einer natürlichen Retusche unbedingt erhalten bleiben müssen. Die beiden größeren Wellen sind z.B. Druckstellen von der Kleidung auf den Babybauch, die in der Retusche verschwinden sollen. Desweiteren wird das Bild von links nach rechts heller, vielleicht weil wir den Babybauch durch Licht-Schatten-Effekte in Szene setzten wollen.
Ebenso könnten wir uns einen anderen Anwendungsfall vorstellen: eine Braut steht am Fenster, die feinen Details sind Maschen im Stoff, die beiden größeren Wellen sind Falten im Kleid, und der Hell-Dunkel-Verlauf kommt durch das seitliche Licht vom Fenster zustande.
Die drei Strukturen entsprechen den drei Bestandteilen 0.1\sin(20x), 0.3\sin(x) und 0.16x-0.96 von \mathrm{B}.
Wir möchten nun die Druckstellen herausretuschieren und dabei die feinen Details und den Hell-Dunkel-Verlauf erhalten. Hierzu wäre es wünschenswert, die drei Anteile seperat zu bearbeiten. Leider liefert uns der Kamerasensor keinen Funktionsterm, den wir in seine Bestandteile zerlegen können. Stattdessen liegt uns \mathrm{B} als gigantische Zahlenkolonne vor…
Wir können nun versuchen, die Retusche mit einem Gaußschen Weichzeichner zu bewerkstelligen. So experimentieren wir mit verschieden Stärken.
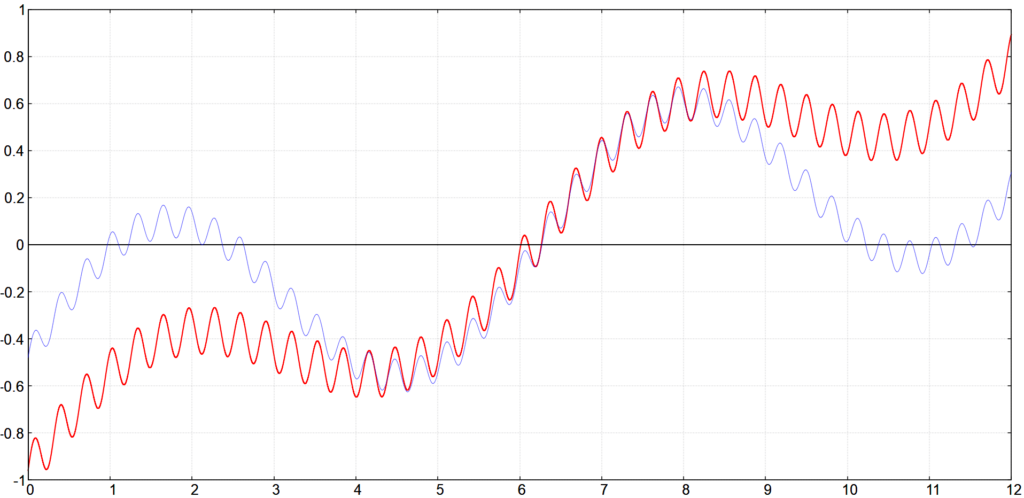
Die originale Funktion \mathrm{B} ist rot, die weichgezeichneten Funktionen sind blau eingezeichnet.
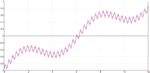
Bei \sigma=0.05 haben wir die Poren schon etwas in Mitleidenschaft gezogen, an den Druckstellen hat sich nichts getan.
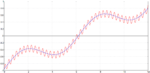
Bei \sigma=0.16 sind die Poren dem Weichzeichner komplett zum Opfer gefallen, allerdings haben wir an den Druckstellen keine sichtbaren Ergebnisse erreicht. An einem realen Bild würden wir damit eine porenfreie, gummiartig geglättete Haut erhalten.
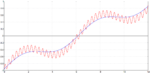
Am letzten Bild erkennen wir, dass erst bei \sigma=1 sichtbare Ergebnisse an den Druckstellen erzielt werden.
Mit dem Gaußschen Weichzeichner schaffen wir es nicht, die Druckstellen zu reduzieren und gleichzeitig die Poren zu erhalten. Wir könnten nun andere Retuschiertechniken versuchen. Mit dem in Mode gekommenen bilateralen Weichzeichner würden wir keine besseren Ergebnisse erzielen. Mit dem Kopierstempel bräuchten wir eine geeignete Quelle, was wegen des Hell-Dunkel-Verlaufes schwierig ist und außerdem, je nach Deckkraft, zu einem statistischen Auslöschen der Poren führen würde.
Der ideale Weg bestünde darin, das Bild in die drei Strukturen 0.1\sin(20x), 0.3\sin(x) und 0.16x-0.96 zu zerlegen.
Schauen wir uns zunächst etwas genauer an, wie ein Gaußscher Weichzeichner auf eine Funktion \sin(nx) wirkt. Durch das Weichzeichnen erhalten wir ein neues Bild w. Dabei ist eine Stelle w(x) definiert als das gewichtete arithmetisches Mittel über die gesamte x-Achse:
\begin{equation*}w(x)\,=\,\int\limits_{\hspace*{-1em}-\infty}^{+\infty\hspace*{-1em}} \underbrace{\raisebox{-3ex}{}\frac{1}{\sigma\sqrt{2\pi}}\;\mathrm{e}^{-\frac{1}{2}(\frac{z-x}{\sigma})^2}}_{\mathrm{(*)}} \sin(nz)\mathrm{d}z\;=\;\mathrm{e}^{-\frac{n^2\sigma^2}{2}}\sin(nx). \end{equation*}
Dabei ist (*) (die Wichtung des arithmetischen Mittels) die Dichtefunktion der Gaußschen Normalverteilung, die einige von uns noch von dem letzten 10DM-Schein kennen. Wir erkennen nun, dass w gerade \sin(nx) mit dem Faktor \mathrm{e}^{-\frac{n^2\sigma^2}{2}} ist. Der Exponent ist offensichtlich immer kleiner als 0, somit liegt der Faktor stets zwischen 0 und 1. Dadurch dämpft der Faktor die Sinusschwingung und wir wollen \mathrm{e}^{-\frac{n^2\sigma^2}{2}} den Dämpfungsfaktor nennen.
Als konkretes Beispiel wollen wir die Funktionen \sin(20x) und \sin(x) mit \sigma=1.6 weichzeichnen und den Wert an der Stelle x=7.9 untersuchen.
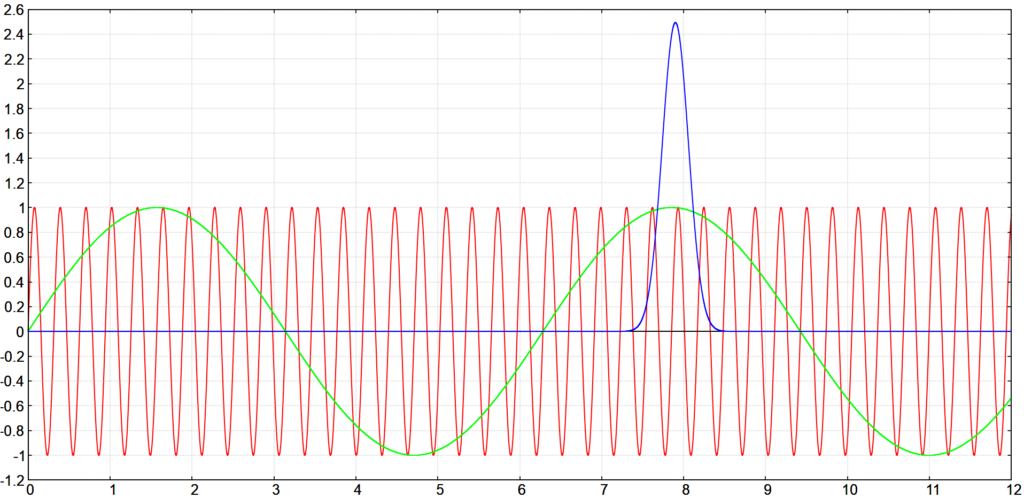
Wenn wir das obige Integral betrachten, dann sind die Bereiche wesentlich, in denen sich die Dichtefunktion deutlich über die x-Achse erhebt, also in etwa der Bereich zwischen 7.4 und 8.4.
Wenn wir nun \sin(20x) (den roten Graphen) weichzeichnen, dann erkennen wir, dass sich im Bereich der hohen blauen Kurve mehrere positive als auch negative Halbwellen von \sin(20x) befinden. Diese löschen sich im Integral gegenseitig weitgehened aus, wodurch das Integral sehr klein wird. Tatsächlich beträgt der Dämpfungsfaktor \mathrm{e}^{-\frac{n^2\sigma^2}{2}}\,=\,\mathrm{e}^{-5.12}\,\approx\,0.006 wodurch der Weichzeichner den Graphen glattbügelt.
Wenn wir nun \sin(x) (den grünen Graphen) weichzeichnen, dann befinden sich auschließlich große, positive Werte im wesentlichen Bereich. Eine Auslöschung findet kaum statt, der Wert des Integrals ist fast so groß wie der Wert von \sin(x). Tatsächlich beträgt der Dämpfungsfaktor nun \mathrm{e}^{-\frac{n^2\sigma^2}{2}}\,=\,\mathrm{e}^{-0.0128}\,\approx\,0.987. Somit verändert sich der Graph beim Weichzeichnen fast nicht.
Somit ist klar, dass feine Details beim Weichzeichnen stärker reduziert werden als grobe Details. Wenn wir beim Weichzeichnen von \sin(nx) den Wert von n verdoppeln, dann wirkt sich das beim Dämpfungsfaktor in der 4. Potenz aus, d.h. wenn \sin(nx) auf den Faktor 0.5 gedämpft wird, dann wird \sin(2nx) auf den Faktor 0.5^4=0.0625 gedämpft.
Mathematisch würde genau das gleiche passieren, wenn wir beim Weichzeichner \sigma verdoppeln.
Jetzt zeichnen wir unser obiges Bild \mathrm{B} mit \sigma=1.6 weich:
\newcommand{\B}{\textrm{B}}\begin{equation*} \B_w(x)\,=\,\int\limits_{\hspace*{-1em}-\infty}^{+\infty\hspace*{-1em}} \frac{1}{\sigma\sqrt{2\pi}}\;\mathrm{e}^{-\frac{1}{2}(\frac{z-x}{\sigma})^2} \big(0.1\sin(20z)+0.3\sin(z)+0.16z-0.96\big)\mathrm{d}z\;=\;\dots\end{equation*}
\begin{equation*}\dots\;=\;\mathrm{e}^{-5.12}\cdot 0.1\sin(20x)+\mathrm{e}^{-0.0128}\cdot 0.3\sin(x)+0.16x-0.96. \end{equation*}
Ich habe nicht vergessen, den linearen Anteil zu integrieren, dieser hat das Integrieren unbeschadet überstanden, er wurde also gar nicht gedämpft.
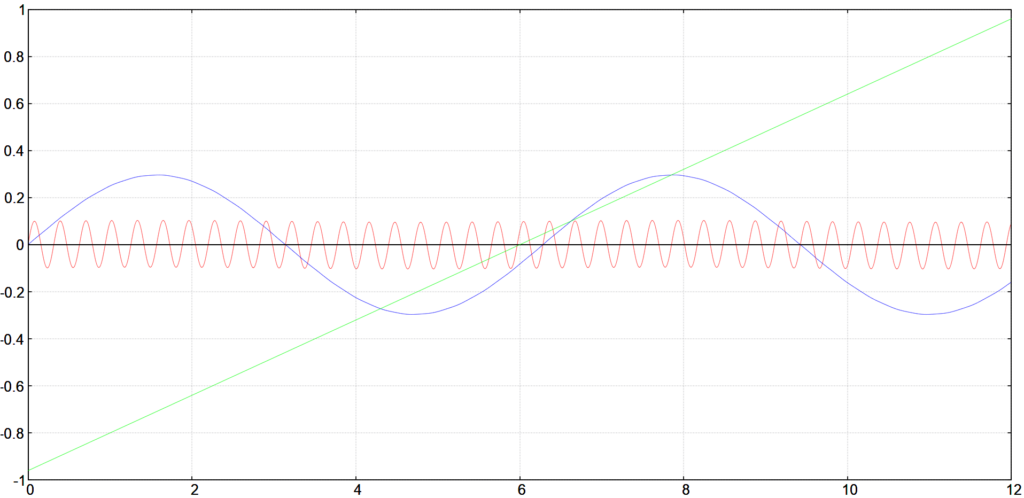
Wir erkennen die beiden Dämpfungsfaktoren \mathrm{e}^{-5.12}\,\approx\,0.006 und \mathrm{e}^{-0.0128}\,\approx\,0.987 wieder. Wir haben also mit \mathrm{B}_w ein Bild, in dem der Weichzeichner die feinen Details entfernt hat, die anderen Strukturen aber noch enthalten sind. Wenn wir jetzt \newcommand{\B}{\textrm{B}}\begin{equation*} \underline{\B_0(x)}\;=\;\B(x)-\B_w(x)\;\approx\;0.994\cdot 0.1\sin(20x) + 0.013\cdot 0.3\sin(x)\;\approx\;\underline{0.1\sin(20x)}\end{equation*}
setzen, dann haben wir mit \mathrm{B}_0 ein Bild, in dem nur noch die feinen Details (also die Poren) enthalten sind.
Wir führen den gleichen Prozess mit \mathrm{B}_0 und \sigma=4 durch:
\newcommand{\B}{\textrm{B}}\begin{equation*} \B_{ww}(x)\,=\,\int\limits_{\hspace*{-1em}-\infty}^{+\infty\hspace*{-1em}} \frac{1}{\sigma\sqrt{2\pi}}\;\mathrm{e}^{-\frac{1}{2}(\frac{z-x}{\sigma})^2} \,\B_w(x)\,\mathrm{d}z\;=\;\dots\end{equation*}
\begin{equation*} \dots\;=\;\mathrm{e}^{-3205.12}\cdot 0.1\sin(20x)+\mathrm{e}^{-8.0128}\cdot 0.3\sin(x)+0.16x-0.96 \end{equation*}
Da beide Dämpfungsfaktoren verschwindend gering sind, enthält \mathrm{B}_{ww} faktisch nur noch den linearen Anteil. Wenn wir wiederum die Differenz bilden\newcommand{\B}{\textrm{B}}\begin{equation*} \underline{\B_1(x)}\;=\;\B_w(x)-\B_{ww}(x)\;\approx\;\underline{0.3\sin(x)},\end{equation*}
dann erhalten wir ein Bild \mathrm{B}_1, welches nur noch die Druckstellen enthält. Zu Vereinheitlichung setzen wir
\newcommand{\B}{\textrm{B}}\begin{equation*} \underline{\B_2(x)}\;=\;\B_{ww}(x)\;\approx\;\underline{0.16x-0.96}\end{equation*}
und es gilt \newcommand{\B}{\textrm{B}}\begin{equation*}\B(x)\;=\;\B_0(x)+\B_1(x)+\B_2(x).\end{equation*}
Damit haben wir das Kunststück geschafft, \mathrm{B} in drei Schichten zu zerlegen, die jeweils die feinen, mittleren und groben Details enthalten. Da \mathrm{B}_0 mit \sin(20x) gewissermaßen eine „höhere Frequenz“ als \mathrm{B}_1 mit \sin(x) hat, können wir von einer „Frequenztrennung“ oder „frequenzseparierten (Haut)retusche“ sprechen.
Jetzt ist es natürlich naheliegend, \mathrm{B}_1 einfach wegzulassen, und die Summe \textrm{B}_0(x)+\textrm{B}_2(x) zu bilden. Dann erhalten wir ein Bild, welches die feinen Details und die groben Sturkturen, jedoch nicht die mittleren Strukturen enthält.
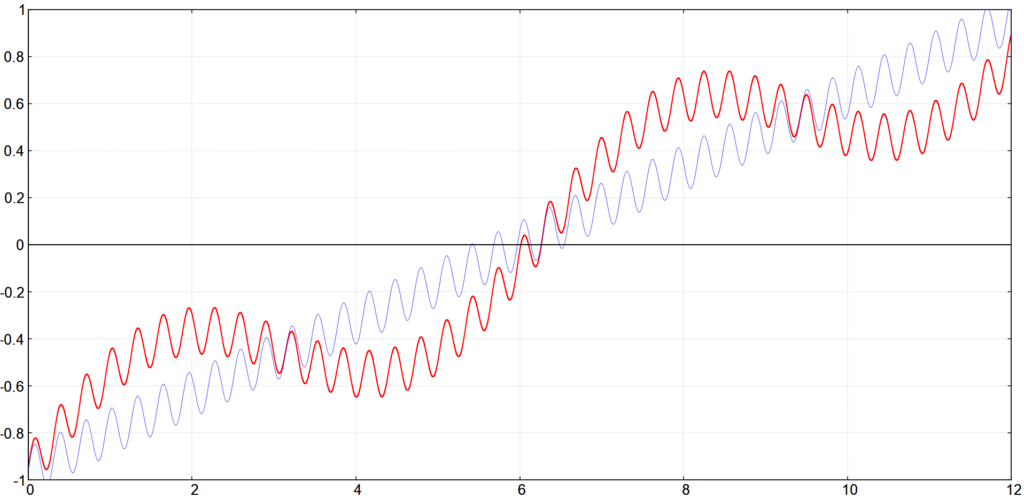
Ebenso können wir die feinen Strukturen und den Hell-Dunkel-Verlauf abschwächen, die mittleren Strukturen verstärken und z.B. die Linearkombination 0.7\cdot\textrm{B}_0(x)+1.5\cdot\textrm{B}_1(x)+0.5\cdot\textrm{B}_2(x) zu bilden. Auf diese Weise könnten wir z.B. die Falten des Brautkleids am Fenster effektvoll in Szene setzen.